
- - or -
Measurement step advanced concepts
This section presents advanced information regarding concepts and settings in the Measurement step. The level of detail described below, such as changing the weighting or relative importance of every aspect of edge determination, is typically not required for designing the majority of applications.

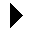 Search algorithm
Search algorithm
Many settings in the Measurement step affect the search algorithm, which is used to identify edge and stripe markers in the search box. For example, Edge threshold, Filter, and Smoothness. In certain cases, understanding the search algorithm can help you make adjustments to such settings, resulting in a more accurate and robust measurement application.

 Identifying
edges
Identifying
edges
To identify edges, the following algorithm is performed:
-
The search algorithm projects the pixels bounded by the specified 2-dimensional search box into a one-dimensional pixel summation, storing the projection result internally (that is, it takes the box's profile). The pixel summation is performed horizontally or vertically, depending on the search direction. Each sum represents the intensity of all the pixels in that column.
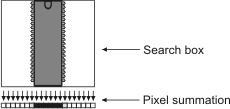
-
The search algorithm applies a first derivative filter to the internally stored projection (pixel summation). The filter finds the edge value of each projection value. The greater the difference in neighboring projection values, the larger the edge value. Edge values are represented as a normalized percentage of the maximum pixel value possible for the specific image.
-
The search algorithm then identifies possible edges by their edge strength; that is, their maximum/minimum edge value depending on the polarity of the edge represented by the sign of the edge value. It rejects as possible marker occurrences any edge with an edge strength below the edge threshold value (Edge threshold setting).
Note that the Edge threshold can be raised to disregard weak edges. However if your search box is not parallel with your edge, raising the threshold might cause the edge not to be found.
-
The search algorithm then scores each possible edge based on geometric constraints that you specify. The edge(s) with the greatest score is returned as an occurrence of the marker.

 First derivative
filter
First derivative
filter
The first derivative filter extracts the difference in neighboring projection values. The edge value calculated for each projection value of the search box is dependent on the type of first derivative filter used to perform the edge extraction: a Finite Impulse Response (FIR) filter, or an Infinite Impulse Response (IIR) filter.
FIR filters are implemented using a non-recursive convolution operation with a predefined kernel of the specified size. To use an FIR filter, set the Filter property to Euler or Prewitt.
IIR filters are implemented using a recursive convolution operation; in this case, the kernel size would be, in theory, infinite (this filter does not however use a kernel). To use an IIR filter, set the Filter property to Shen (default), and specify the strength of denoising applied to the internal projection result, using the Smoothness property. By default, the smoothness is set to 50.
You can experiment with these filters to find which best suits your application needs. The following is the general characteristics of each filter:
-
Euler. This is an FIR filter with a convolution kernel of size 2: [-1,1]. This filter is faster but more sensitive to noise, compared to the Prewitt filter.
-
Prewitt. This is an FIR filter with a convolution kernel of size 3: [-1,0,1]. This filter is slower but less sensitive to noise, compared to the Euler filter.
-
Shen. This is a Shen-Castan Infinite Support Exponential filter, which is an IIR filter. This is an exponential weighting function, of the general form:
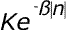
This IIR filter is slower than FIR filters (Euler or Prewitt). However, this filter is less sensitive to noise and provides more accurate results. It also allows you to control the strength of denoising (Smoothness).